All Stacks Developer

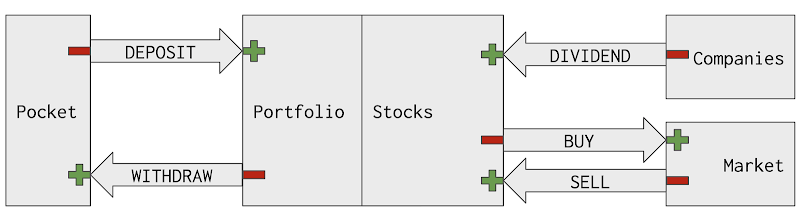
As a long-term investor, I need to know how to evaluate the performance of my stock portfolio. A simple return on investment calculation is not a good indicator for long-term investment because it does not take into account the holding duration, and cash flows involved during that period. A return on investment of 80% after 20 years is not as impressive as it sounds after 1 year. In this post, I explain the idea of using Google Sheets to calculate the internal rate of return (IRR) and the net present value (NPV) of a stock portfolio.

Why do I use my current money to invest in the stock market? Because I expect to have more money in the future. Why do I need more money in the future than now? Because of many reasons, the same amount of money will have less purchasing power than today. Therefore my investment needs to generate more money than today to protect my purchasing power in the future. That is the main concept of the time value of money where one dollar today is worth more than one dollar in the future.