Time value of money, Present Value (PV), Future Value (FV), Net Present Value (NPV), Internal Rate of Return (IRR)

Why do I use my current money to invest in the stock market? Because I expect to have more money in the future. Why do I need more money in the future than now? Because of many reasons, the same amount of money will have less purchasing power than today. Therefore my investment needs to generate more money than today to protect my purchasing power in the future. That is the main concept of the time value of money where one dollar today is worth more than one dollar in the future.

Present Value (PV), Future Value (FV)
Net Present Value (NPV)
Discount rate
Internal Rate of Return (IRR)
Conclusion
Series: how to calculate internal rate of return (IRR) and net present value (NPV) for a stock portfolio in Google Sheets
Disclaimer
Feedback
Support this blog
Share with your friends

Present Value (PV), Future Value (FV)

At 10% annual growth rate, an investment of 1000$ will be worth 1000 * 110% = 1100$ after 1 year, and will be worth 1000 * 110% * 110% = 1210$ after 2 years.

The future value of 1000$ after 2 years at the rate of 10% is 1210$.
Inversely, the "present value" of 1210$ 2 years ago at the rate of 10% is 1000$.

Benchmark a stock investment portfolio with a compound interest saving account in Google Sheets

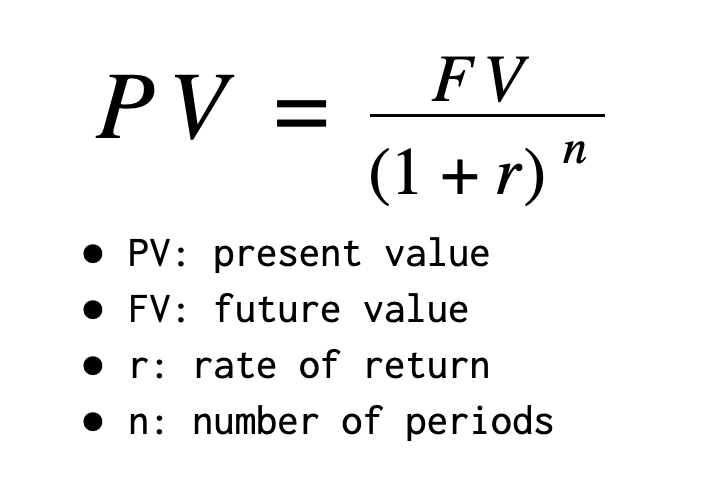
Net Present Value (NPV)

Let's say I have 1000$ now and a bank offers me a saving account at a 10% annual rate. At the same time, a public company attracts my attention because it pays a very good amount of dividend each year and has potential growth in the future. The scenario is that I would buy 100 shares at the cost of 10$ each now and hold them for 5 years. Each year I would receive a fairly good and stable amount of dividends, at least 5% yield. After 5 years, I would sell all shares with the expectation that the share price would grow 20%. The table below shows the scenario of cash flows if I buy stocks of that company. Which investment should I choose?

Year	Amount	Type
0	-$1,000.00	Buy
1	$50.00	Dividend
2	$55.00	Dividend
3	$60.00	Dividend
4	$65.00	Dividend
5	$1,200.00	Sell

To make that decision, let put it this way: I want to have the same scenario of cash flows as investing into the stock market but by putting money into a saving account at a 10% annual rate. How much money do I need to put into that saving account now? Let's do the math:

At a 10% rate, to have 50$ after 1 year, I need to invest 45.45$ now. Because 50$ is the future value of 45.45$ after 1 year at a 10% rate.
At a 10% rate, to have 55$ after 2 years, I need to invest 45.45$ now. Because 55$ is the future value of 45.45$ after 2 years at a 10% rate.
At a 10% rate, to have 60$ after 3 years, I need to invest 45.08$ now. Because 60$ is the future value of 45.08$ after 3 years at a 10% rate.
At a 10% rate, to have 65$ after 4 years, I need to invest 44.40$ now. Because 65$ is the future value of 44.40$ after 4 years at a 10% rate.
At a 10% rate, to have 1200$ after 5 years, I need to invest 745.11$ now. Because 1200$ is the future value of 745.11$ after 5 years at a 10% rate.

Totally, to have the same scenario of cash flows as investing in the stock market, I need to invest 45.45 + 45.45 + 45.08 + 44.40 + 745.11 = 925.49$ now in a saving account at a 10% rate. In other words, to have the same result in the future, investing in the stock market costs me 1000$ now, whereas investing in the saving account at a 10% rate costs me only 925.49$ now. Therefore, in this case, I should better put money in the saving account at 10% rate.

Let's suppose that the share prices would grow 50% during the 5 years, which means the last cash flow would be 1500$ in the 5th year. In this case, at a 10% rate, to have 1500$ after 5 years, I need to invest 931.38$ now. Because 1500$ is the future value of 931.38$ after 5 years at a 10% rate. Totally, to have the same scenario of cash flows as investing in the stock market, I need to invest 45.45 + 45.45 + 45.08 + 44.40 + 931.38 = 1089.88$ now in a saving account at a 10% rate. In other words, to have the same result in the future, investing in the stock market costs me only 1000$ now, whereas investing into the saving account at a 10% rate costs me 1089.88$ now. Therefore, in this case, I have a better deal to invest in the stock market than to put money in a saving account at a 10% rate.

Moreover, because at year 0 future value equals to present value, I can do like that:

For the first scenario, sum of all present values of future cash flows is: -1000 + 45.45 + 45.45 + 45.08 + 44.40 + 745.11 = -96.40 < 0
For the second scenario, sum of all present values of future cash flows is: -1000 + 45.45 + 45.45 + 45.08 + 44.40 + 931.38 = 89.88 > 0

What's I have calculated so far is to sum the present values of future cash flows at a defined discount rate and compare it with 0. That's what they call Net Present Value (NPV). If Net Present Value (NPV) is positive, the investment is worth pursuing.

Discount rate

In this example, I have chosen the saving account at a 10% annual rate as a benchmark to evaluate my investment in the stock market. The 10% annual rate of that saving account is therefore the discount rate in my evaluation. My investment in the stock market must beat 10% annually, otherwise, it is not worth my time and effort because I can easily save that money at 10% annually. The choice of a discount rate is important and depends on personal preferences. Here are a few examples:

A minimum required rate of return for an investment that one sets for herself/himself
An expected rate of return if investing in an alternative asset such as: saving account, real estate, buying a business, etc.
A reference rate of return of the market: S&P 500, CAC 40, etc.

Internal Rate of Return (IRR)

The discount rate that makes Net Present Value (NPV) equal to zero is called the Internal Rate of Return (IRR).

For the first scenario of cash flows above, that internal rate of return is 8.13%.
- At a 8.13% rate, sum of all present values of future cash flows is: -1000 + 46.24 + 47.04 + 47.46 + 47.54 + 811.72 = 0.
- Because 8.13% < 10%, it confirms once again that the saving account at a 10% rate is a better choice.

Year	Amount	Type	Present Value
0	-$1,000.00	Buy	-$1,000.00
1	$50.00	Dividend	$46.24
2	$55.00	Dividend	$47.04
3	$60.00	Dividend	$47.46
4	$65.00	Dividend	$47.54
5	$1,200.00	Sell	$811.72

For the second scenario of cash flows above, that internal rate of return is 12.57%.
- At a 12.57% rate, sum of all present values of future cash flows is: -1000 + 44.42 + 43.40 + 42.06 + 40.47 + 829.66 = 0.
- Because 12.57% > 10%, it confirms once again that investing in the stock market is a better choice.

Year	Amount	Type	Present Value
0	-$1,000.00	Buy	-$1,000.00
1	$50.00	Dividend	$44.42
2	$55.00	Dividend	$43.40
3	$60.00	Dividend	$42.06
4	$65.00	Dividend	$40.47
5	$1,500.00	Sell	$829.66

Conclusion

In summary, Net Present Value (NPV) and Internal Rate of Return (IRR) are two methods that help me to evaluate the performance of an investment.

To evaluate an investment with Net Present Value (NPV), I follow the steps below:

Identify all cash flows
Pick a discount rate
Calculate Net Present Value (NPV) by summing all present values of those cash flows
If Net Present Value (NPV) is positive, the investment is worth pursuing

To evaluate an investment with Internal Rate of Return (IRR), I follow the steps below:

Identify all cash flows
Pick a discount rate
Calculate the Internal Rate of Return (IRR) rate that makes Net Present Value (NPV) equal to 0
If Internal Rate of Return (IRR) is bigger than the discount rate, the investment is worth pursuing

Performing those steps requires many calculations, and I don't perform them manually. I have leveraged the built-in functions of Google Sheets to do those tasks. In the next posts, I will explain how to calculate Net Present Value (NPV) and Internal Rate of Return (IRR) in Google Sheets, particularly in the context of a stock portfolio.