How to convert column index into letters with Google Apps Script

Although Google Sheets does not provide a ready-to-use function that takes a column index as an input and returns corresponding letters as output, we can still do the task by leveraging other built-in functions ADDRESS, REGEXEXTRACT, INDEX, SPLIT as shown in the post. However, in form of a formula, that solution is not applicable for scripting with Google Apps Script. In this post, we look at how to write a utility function with Google Apps Script that converts column index into corresponding letters.

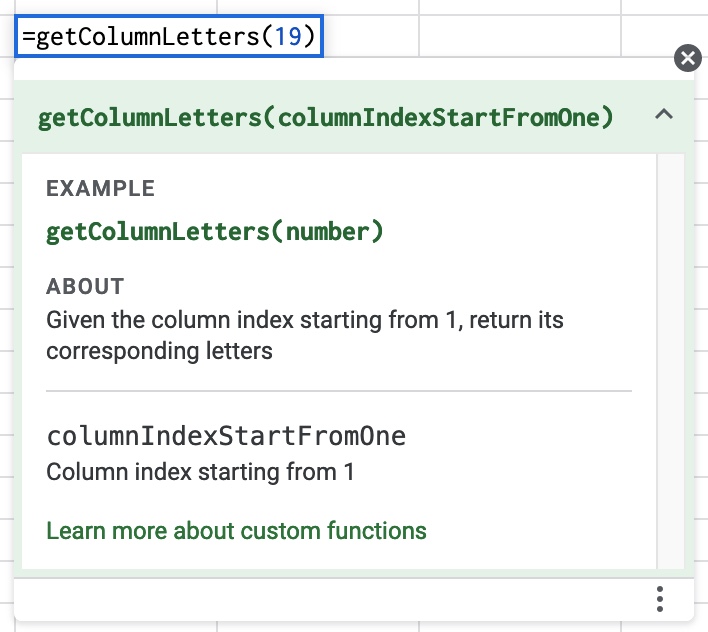
Table of Contents

• Concept
• Demo
• Disclaimer
• Feedback
• Support this blog
• Share with your friends

Concept

With the solution in the form of a formula, we don't even need to understand how column index and letters map each other. With apps script, we need to understand the mapping to come up with an algorithm.

In a spreadsheet, columns are indexed alphabetically, starting from A.

• Obviously, the first 26 columns correspond to 26 alphabet characters, A to Z.
• The next 676 columns (26*26), from 27th to 702nd, are indexed with 2 letters. [AA, AB, ... AY, AZ], [BA, BB, ... BY, BZ], ... [MA, MB, ... MY, MZ], ... [ZA, ZB, ... ZY, ZZ]. Each alphabet character takes a turn (in order) to precede all 26 alphabet characters.
• The next 17576 columns (26*26*26), from 703rd to 18278th, are indexed with 3 letters. [AAA, AAB, ... AAY, AAZ], [ABA, ABB, ... ABY, ABZ], ... [ZZA, ZZB, ... ZZY, ZZZ]. Each letter AA to ZZ above takes a turn (in order) to precede all 26 alphabet characters.
• etc.

The above observation suggests a recursive pattern. Columns with 3 letters depend on columns with 2 letters, columns with 2 letters depend on columns with 1 letter. Moreover, the number of letters for a column depends on its index divided by 26. It suggests that we need to divide column index by 26 to apply the recursive pattern. So, here are the steps of the algorithm:

• let ALPHABETS=['A', 'B', 'C', 'D', ... 'X', 'Y', 'Z']
• if k <= 26, then return ALPHABETS[k - 1];
• else return getColumnLetters(k / 26) + ALPHABETS[(k % 26) - 1]

Column Index	Column Letters	Divide by 26
12	L	=12
13	M	=13
26	Z	=26
27	AA	=1*26+1
37	AK	=1*26+11
38	AL	=1*26+12
53	BA	=2*26+1
75	BW	=2*26+23
988	AKZ	=37*26+26
989	ALA	=38*26+1
1390	BAL	=53*26+12
1963	BWM	=75*26+13

Let's take the column 1963rd as an example:

• As 1963=75*26+13, the 1963rd column letters are the concatenation of the 75th column letters and the 13th column letters.
  • As 13 < 26, the 13rd column's letter is the 13rd alphabet character that is M.
  • As 75 = 2 * 26 + 23, the 75th column letters are the concatenation of the 2nd column letters and the 23rd column letters.
    • As 2 < 26, the 2nd column letter is the 2nd alphabet character that is B.
    • As 23 < 26, the 23rd column letter is the 23rd alphabet character that is W.
    • The 75th column letters are hence B + W = BW.
  • The 1963rd column letters are hence BW + M = BWM.

Let's analyze the column 988th that is a little bit trickier because 988 is divisible by 26:

• As 988=38*26+0, the 988th column letters are the concatenation of the 38th column letters and the 0th column letters. But wait, column index starts from 1, doesn't it?.
  • In fact, as 988 is divisible by 26, it can be expressed as 988=37*26+26. That means the 988th column letters are the concatenation of the 37th column letters and the 26th column letters.
  • As 26 = 26, the 26th column letter is the 26th alphabet character that is Z.
  • As 37 = 1 * 26 + 11, the 37th column letters are the concatenation of the 1st column's letter and the 11th column's letter.
    • Because, 1 < 26, the 1st column letter is the 1st alphabet character that is A.
    • As 11 < 26, the 11th column letter is the 11th alphabet character that is K.
    • The 37th column letters are hence A + K = AK.
  • The 988th column letters are hence AK + Z = AKZ.

To implement this algorithm in javascript, we need to pay attention to certain points:

• The column index, which is the input of the function, starts from 1, while the array in javascript starts from 0.
• When dividing the column index by 26, we need to round the result down.
• If the column index is divisible by 26, the residual is 0. To apply the next recursive call, we need to reduce the result by one while increasing the residual by 26.

Demo

Finally, you can find below an example of code to convert column index into corresponding letters in Google Apps Script and a test function that prints out letters for all the first 1000 columns in 3 different ways that we have discovered in these 2 posts.

function getColumnLetters(columnIndexStartFromOne) {
  const ALPHABETS = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']

  if (columnIndexStartFromOne < 27) {
    return ALPHABETS[columnIndexStartFromOne - 1]
  } else {
    var res = columnIndexStartFromOne % 26
    var div = Math.floor(columnIndexStartFromOne / 26)
    if (res === 0) {
      div = div - 1
      res = 26
    }
    return getColumnLetters(div) + ALPHABETS[res - 1]
  }
}

function test() {
  var rows = []
  var row1 = []
  var row2 = []
  var row3 = []
  var row4 = []
  for(let i = 1; i < 1000; i++) {
    row1.push(getColumnLetters(i))
    row2.push(i)
    row3.push('=REGEXEXTRACT(ADDRESS(1, ' + i + '),"\\$([A-Za-z]+)\\$")')
    row4.push('=INDEX(SPLIT(ADDRESS(1, ' + i + '),"$"),1,1)')
  }
  rows.push(row1, row2, row3, row4)

  var sheetName = "test"
  var spreadsheet = SpreadsheetApp.getActive()
  var sheet = spreadsheet.getSheetByName(sheetName)
  if (sheet) {
    sheet.clear()
  } else {
    sheet = spreadsheet.insertSheet(sheetName, spreadsheet.getNumSheets())
  }
  sheet.getRange(1, 1, rows.length, rows[0].length).setValues(rows)
}

Disclaimer

The post is only for informational purposes and not for trading purposes or financial advice.

Feedback

If you have any feedback, question, or request please:

• leave a comment in the comment section
• write me an email to allstacksdeveloper@gmail.com

Support this blog

If you value my work, please support me with as little as a cup of coffee! I appreciate it. Thank you!

Share with your friends

If you read it this far, I hope you have enjoyed the content of this post. If you like it, share it with your friends!